- К-ТЕОРИЯ
-
К-ТЕОРИЯ
К-ТЕОРИЯ — ветвь алгебраической топологии, начало и бурное развитие которой относится к последним двум десятилетиям.
Исходным объектом этой теории является векторное расслоение над конечным клеточным комплексом. Пусть
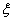 и
и 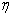 — два векторных расслоения над СW-комплексом. Эти расслоения (пучки) называются стабильно эквивалентными, если существует такое натуральное число
— два векторных расслоения над СW-комплексом. Эти расслоения (пучки) называются стабильно эквивалентными, если существует такое натуральное число 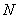 , что расслоения
, что расслоения 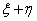 и
и 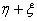 эквивалентны как векторные расслоения. Здесь
эквивалентны как векторные расслоения. Здесь 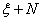 ,
, 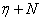 означают векторные расслоения, равные суммам Уитни расслоений
означают векторные расслоения, равные суммам Уитни расслоений 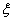 и
и 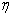 с тривиальным векторным расслоением размерности
с тривиальным векторным расслоением размерности 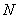 .
.Множество классов эквивалентных векторных расслоений над
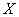 , факторизованное по отношению стабильной эквивалентности, порождает кольцо (над целыми числами). Его обозначают
, факторизованное по отношению стабильной эквивалентности, порождает кольцо (над целыми числами). Его обозначают 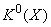 . Операция сложения элементов
. Операция сложения элементов 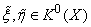 порождается суммой Уитни расслоений
порождается суммой Уитни расслоений 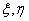 — представителей классов стабильно эквивалентных пучков
— представителей классов стабильно эквивалентных пучков 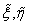 .
.Корректность операции вычитания элементов
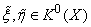 обусловлена следующим фактом из теории векторных расслоений: для каждого расслоения
обусловлена следующим фактом из теории векторных расслоений: для каждого расслоения 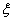 над
над 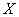 существует такое расслоение
существует такое расслоение 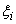 , что сумма Уитни
, что сумма Уитни 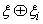 является тривиальным векторным расслоением
является тривиальным векторным расслоением 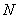 (т. е. тривиальным расслоением размерности
(т. е. тривиальным расслоением размерности 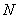 ) над
) над 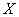 . При
. При 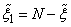 и
и 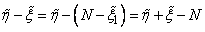 (волна над
(волна над 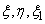 , означает класс стабильной эквивалентности, соответствующий
, означает класс стабильной эквивалентности, соответствующий 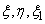 ).
).Умножение элементов из
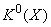 порождено тензорным умножением векторных расслоений.
порождено тензорным умножением векторных расслоений.Описанное построение кольца
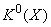 называется конструкцией Гротендика. Идея этой конструкции лежит в основании К.т. В дальнейшем описании К. т. ограничимся случаем комплексных векторных расслоений — комплексная К. т.
называется конструкцией Гротендика. Идея этой конструкции лежит в основании К.т. В дальнейшем описании К. т. ограничимся случаем комплексных векторных расслоений — комплексная К. т.Фундаментальным фактором этой теории является периодичность Р. Ботта. Теорема Ботта о периодичности устанавливает изоморфизм
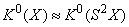 как аддитивных групп, т. е. взаимно однозначное соответствие элементов
как аддитивных групп, т. е. взаимно однозначное соответствие элементов 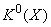 ,
, 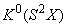 , сохраняющее операцию сложения. Здесь
, сохраняющее операцию сложения. Здесь 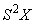 означает двойную надстройку над пространством
означает двойную надстройку над пространством 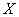 .
.Пусть
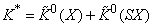 , где
, где 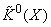 означает множество элементов
означает множество элементов 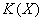 размерности нуль (
размерности нуль (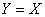 ,
, 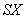 ). При этом
). При этом 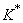 (с учетом изоморфизма Ботта) оказывается кольцом, закон умножения в котором удовлетворяет условию
(с учетом изоморфизма Ботта) оказывается кольцом, закон умножения в котором удовлетворяет условию 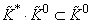 ,
, 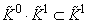 ,
, 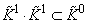 , здесь
, здесь 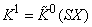 .
.Каждое векторное расслоение
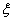 размерности
размерности 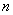 над
над 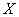 удобно описывается с помощью так называемого характеристического отображения:
удобно описывается с помощью так называемого характеристического отображения: 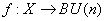 , где
, где 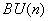 — универсальное пространство — множество n-мерных плоскостей в N-мерном эрмитовом линейном пространстве, проходящих через начало координат. (Чему равно
— универсальное пространство — множество n-мерных плоскостей в N-мерном эрмитовом линейном пространстве, проходящих через начало координат. (Чему равно 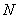 — несущественно, важно только, что
— несущественно, важно только, что 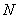 велико.)
велико.)Гомотопический класс характеристического отображения определяет расслоение
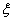 однозначно с точностью до эквивалентности. Топологически пространство
однозначно с точностью до эквивалентности. Топологически пространство 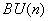 хорошо изучено. Его кольцо когомологий изоморфно кольцу симметрических многочленов от
хорошо изучено. Его кольцо когомологий изоморфно кольцу симметрических многочленов от 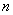 переменных
переменных 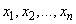 , каждому из которых приписана степень два. Образующие этого кольца — элементарные симметрические полиномы
, каждому из которых приписана степень два. Образующие этого кольца — элементарные симметрические полиномы 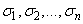 — порождают классы
— порождают классы 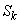 когомологий пространства
когомологий пространства 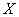 по формуле
по формуле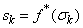 ,
,где антиотображение когомологий
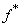 соответствует характеристическому отображению
соответствует характеристическому отображению 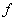 . Элемент
. Элемент  называется k-м классом Черна расслоения
называется k-м классом Черна расслоения 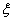 .
.В алгебре когомологий пространства
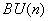 над полем действительных чисел имеется замечательный элемент
над полем действительных чисел имеется замечательный элемент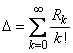
(здесь
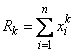 — полиномы Ньютона, они являются многочленами от элементарных симметрических полиномов
— полиномы Ньютона, они являются многочленами от элементарных симметрических полиномов 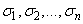 , так что в самом деле принадлежат алгебре когомологий пространства
, так что в самом деле принадлежат алгебре когомологий пространства 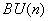 с вещественными коэффициентами). Элемент
с вещественными коэффициентами). Элемент  порождает элемент
порождает элемент 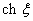 в алгебре когомологий пространства
в алгебре когомологий пространства 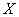 по формуле:
по формуле: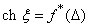 .
.При этом
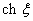 называется характером Черна расслоения
называется характером Черна расслоения 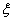 .
.Характер Черна задает отображение
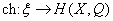 .
.Это отображение индуцирует отображение
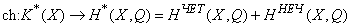 (*)
(*)При этом элементам из
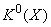 соответствуют четномерные когомологии из
соответствуют четномерные когомологии из 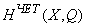 , а элементам из
, а элементам из 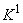 — нечетномерные когомологии из
— нечетномерные когомологии из 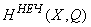 . Это отображение является гомоморфизмом колец
. Это отображение является гомоморфизмом колец 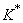 и
и 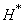 .
.Резюмируем и уточним вышесказанное. Каждому CW-комплексу
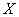 можно поставить в соответствие кольцо
можно поставить в соответствие кольцо 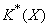 . Это соответствие является контравариантным функтором из категории CW-комплексов и непрерывных отображений в категорию колец и гомоморфизмов. Гомотопически эквивалентным (см. Гомотопическая эквивалентность)
. Это соответствие является контравариантным функтором из категории CW-комплексов и непрерывных отображений в категорию колец и гомоморфизмов. Гомотопически эквивалентным (см. Гомотопическая эквивалентность) 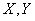 соответствуют изоморфные
соответствуют изоморфные 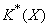 ,
, 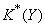 . Это обстоятельство позволяет изучать гомотопические свойства пространства
. Это обстоятельство позволяет изучать гомотопические свойства пространства 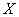 , рассматривая алгебраические свойства колец
, рассматривая алгебраические свойства колец 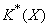 . Отображение (*) связывает К-теорию с теорией когомологий.
. Отображение (*) связывает К-теорию с теорией когомологий.Ввиду того что К-теория построена на основе геометрического понятия векторного расслоения, она оказывается более тонкой характеристикой гомотопического типа пространства
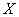 , чем теория когомологий.
, чем теория когомологий.С помощью К-теории в последнее время было получено решение ряда трудных и давно ждавших решения задач: об алгебрах с делением, о векторных полях на сферах и др.
Основные труды по К-теории принадлежат А. Гротендику, Р. Ботту, М. Атье, Дж. Адамсу, С. П. Новикову.
- КАВАЛЬЕРИ ПРИНЦИП
- КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
- КАНОНИЧЕСКОЕ УРАВНЕНИЕ
- КАНТОРА АКСИОМА
- КАНТОРА-БЕРНШТЕЙНА ТЕОРЕМА
- КАНТОРОВО МНОЖЕСТВО
- КАППА
- КАРДАНО ФОРМУЛА
- КАРДИНАЛЬНОЕ ЧИСЛО
- КАРДИОИДА
- КАРНО ТЕОРЕМА
- КАРТА
- КАСАНИЕ
- КАСАТЕЛЬНАЯ
- КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
- КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- КАССИНИ ОВАЛ
- КАТЕГОРИЯ
- КАТЕНОИД
- КАТЕТ
- КАЧЕСТВЕННАЯ ТЕОРИЯ
- КАЧЕСТВЕННЫЕ МЕТОДЫ
- КВАДРАНТ
- КВАДРАТ
- КВАДРАТИЧЕСКАЯ ОШИБКА
- КВАДРАТИЧНАЯ ИРРАЦИОНАЛЬНОСТЬ
- КВАДРАТИЧНАЯ ФОРМА
- КВАДРАТИЧНАЯ ФУНКЦИЯ
- КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ
- КВАДРАТИЧНОЕ СРЕДНЕЕ
- КВАДРАТИЧНЫЕ ЧИСЛА
- КВАДРАТИЧНЫЙ ВЫЧЕТ
- КВАДРАТИЧНЫЙ НЕВЫЧЕТ
- КВАДРАТНАЯ МАТРИЦА
- КВАДРАТНОЕ УРАВНЕНИЕ
- КВАДРАТНЫЙ ТРЕХЧЛЕН
- КВАДРАТРИСА
- КВАДРАТУРА
- КВАДРАТУРНЫЕ ФОРМУЛЫ
- КВАДРИЛЛИОН
- КВАДРИРУЕМАЯ ОБЛАСТЬ
- КВАЗИГРУППА
- КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
- КВАЗИПЕРИОДИЧЕСКИЕ ФУНКЦИИ
- КВАНТОР
- КВАТЕРНИОН
- КЕПЛЕРА УРАВНЕНИЕ
- КИБЕРНЕТИКА
- КЛАВИШНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- КЛАСС
- КЛЕЙНА ИНТЕРПРЕТАЦИЯ
- КЛЕРО УРАВНЕНИЕ
- КЛЕТКА
- КЛЕТОЧНОЕ РАЗБИЕНИЕ
- КЛЕТОЧНЫЙ КОМПЛЕКС
- КЛЕТОЧНЫЙ ПОЛИЭДР
- КЛОТОИДА
- КОВАРИАНТНОСТЬ И КОНТРАВАРИАНТНОСТЬ
- КОДИРОВАНИЕ
- КОЛЕБАНИЕ ФУНКЦИИ
- КОЛИЧЕСТВЕННОЕ ЧИСЛО
- КОЛЛИНЕАРНЫЕ ВЕКТОРЫ
- КОЛЛИНЕАЦИЯ
- КОЛОГАРИФМ
- КОЛЬЦО
- КОЛЬЦО ГЛАВНЫХ ИДЕАЛОВ
- КОЛЬЦО МНОГОЧЛЕНОВ
- КОЛЬЦО С ЕДИНИЦЕЙ
- КОМБИНАТОРИКА
- КОМБИНАТОРНАЯ ТОПОЛОГИЯ
- КОММУТАНТ
- КОММУТАТИВНАЯ ГРУППА
- КОММУТАТИВНОЕ КОЛЬЦО
- КОММУТАТИВНОСТЬ
- КОММУТАТОР
- КОМПАКТ
- КОМПАКТНОСТЬ
- КОМПЛАНАРНЫЕ ВЕКТОРЫ
- КОМПЛЕКС
- КОМПЛЕКС ПРЯМЫХ
- КОМПЛЕКСНАЯ СТРУКТУРА
- КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ФУНКЦИИ
- КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ЧИСЛА
- КОМПЛЕКСНОЕ ЧИСЛО
- КОМПОЗИЦИЯ (СУПЕРПОЗИЦИЯ) ОТОБРАЖЕНИЙ
- КОМПОНЕНТА
- КОНВЕНЦИОНАЛИЗМ
- КОНГРУЭНТНОСТЬ
- КОНГРУЭНЦИЯ
- КОНЕЧНАЯ ГРУППА
- КОНЕЧНООПРЕДЕЛЕННАЯ ГРУППА
- КОНЕЧНОПОРОЖДЕННАЯ (УНИВЕРСАЛЬНАЯ) АЛГЕБРА
- КОНЕЧНЫХ ПРИРАЩЕНИЙ ФОРМУЛА
- КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ
- КОНИЧЕСКАЯ ПОВЕРХНОСТЬ
- КОНИЧЕСКИЕ СЕЧЕНИЯ
- КОНОИД
- КОНСЕКВЕНТ
- КОНСТАНТА
- КОНСТРУКТИВНАЯ ГЕОМЕТРИЯ
- КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИЙ
- КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
- КОНТИНУУМ
- КОНТИНУУМ-ПРОБЛЕМА
- КОНТРАВАРИАНТНОСТЬ
- КОНТРАГРЕДИЕНТНОСТЬ
- КОНТРПАРАЛЛЕЛОГРАММ
- КОНУС
- КОНФИГУРАЦИЯ
- КОНФОКАЛЬНЫЕ КРИВЫЕ
- КОНФОРМНАЯ ГЕОМЕТРИЯ
- КОНФОРМНАЯ ГРУППА
- КОНФОРМНАЯ СВЯЗНОСТЬ
- КОНФОРМНО-ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
- КОНФОРМНОЕ ОТОБРАЖЕНИЕ
- КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ
- КОНФОРМНОЕ ПРОСТРАНСТВО
- КОНФОРМНОЙ СВЯЗНОСТИ ГЕОМЕТРИЯ
- КОНФОРМНОЙ СВЯЗНОСТИ ПРОСТРАНСТВО
- КОНХОИДА
- КОНЦЕНТРИЧЕСКИЕ ОКРУЖНОСТИ
- КОНЪЮНКЦИЯ
- КООРДИНАТНАЯ ОКРЕСТНОСТЬ
- КООРДИНАТНЫЕ ВЕКТОРЫ
- КООРДИНАТЫ
- КООРДИНАТЫ ВЕКТОРА
- КОРЕНЬ ИЗ ЧИСЛА
- КОРЕНЬ МНОГОЧЛЕНА
- КОРЕНЬ УРАВНЕНИЯ
- КОРНЯ СПИРАЛЬ
- КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ
- КОРРЕЛЯЦИЯ
- КОРТЕЖ
- КОСЕКАНС
- КОСЕКАНСОИДА
- КОСИНУС
- КОСИНУС ГИПЕРБОЛИЧЕСКИЙ
- КОСИНУС-ВЕРЗУС
- КОСИНУСОВ ТЕОРЕМА
- КОСИНУСОИДА
- КОСОСИММЕТРИЧЕСКАЯ МАТРИЦА
- КОСОСИММЕТРИЧЕСКИЙ ОПРЕДЕЛИТЕЛЬ
- КОСОСИММЕТРИЧНОСТЬ
- КОСОУГОЛЬНЫЕ КООРДИНАТЫ
- КОТАНГЕНС
- КОТАНГЕНСОИДА
- КОТЕСА ФОРМУЛА
- КОХЛЕОИДА
- КОШИ ЗАДАЧА
- КОШИ КРИТЕРИЙ
- КОШИ-БУНЯКОВСКОГО НЕРАВЕНСТВО
- КОШИ-РИМАНА УРАВНЕНИЯ
- КОЭФФИЦИЕНТ
- КРАЕВАЯ ЗАДАЧА
- КРАЙНИЕ ЧЛЕНЫ
- КРАМЕРА ПРАВИЛО
- КРАТНАЯ ПРОПОРЦИЯ
- КРАТНОЕ
- КРАТНЫЙ ИНТЕГРАЛ
- КРАТНЫЙ КОРЕНЬ
- КРИВАЯ ВТОРОГО ПОРЯДКА
- КРИВИЗНА
- КРИВИЗНЫ ТЕНЗОР
- КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ
- КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
- КРИСТОФФЕЛЯ СИМВОЛЫ
- КРИТЕРИЙ
- КРИТИЧЕСКАЯ ТОЧКА
- КРОНЕКЕРА-КАПЕЛЛИ ТЕОРЕМА
- КРУГ
- КРУГ КРИВИЗНЫ
- КРУГ СХОДИМОСТИ
- КРУГЛЫЕ ТЕЛА
- КРУГЛЫЙ КОНУС
- КРУГЛЫЙ ЦИЛИНДР
- КРУГОВАЯ ТОЧКА
- КРУГОВЫЕ ФУНКЦИИ
- КРУЧЕНИЕ
- КУБ
- КУБИЧЕСКАЯ ПАРАБОЛА
- КУБИЧЕСКОЕ УРАВНЕНИЕ
- КЭЛИ АЛГЕБРА